中国科学与测量与地球物理研究所
胡小刚 薛秀秀 郝晓光
我们利用测地所高精度重力观测数据对3月11日日本仙台9.0级大地震的震源机制和深度进行约束。长期以来,测地所在武汉,拉萨和南极中山站建立了重力观测站(参见图1),利用高精度超导重力仪监测地球的时变重力场。这些高精度重力仪记录到了日本仙台大地震激发的地球自由震荡。地球长周期自由震荡的简正模的振幅大小依赖于地震矩、地震深度、震源断层的破裂方式。自由震荡重力观测数据中包含了地震激发的地面运动和重力场变化。
日本大地震后,多家国际学术机构,如美国usgs、哈佛大学、法国ipgs,利用观测到的地震体波和面波计算了震源机制,地震矩心矩张量,地震深度,给出了矩震级的大小(表1)。根据这些计算结果,我们计算了武汉,拉萨和南极中山站的自由震荡模拟值,将自由震荡的重力观测值与这些模拟值进行比较(图1、2),可对这些机构的计算结果进行鉴定和约束。
表1 日本仙台大地震的地震矩心矩张量、地震深度、震源机制解、震级
|
|
m0 |
mrr |
mtt |
mpp |
mrt |
mrp |
mtp |
depth(km) |
strike (o) |
dip (o) |
slip (o) |
mw |
|
harvard |
5.31 |
1.73 |
-0.281 |
-1.45 |
2.12 |
4.55 |
-0.657 |
20 |
203 |
10 |
88 |
9.1 |
|
usgs1 |
4.50 |
2.03 |
-0.16 |
-1.87 |
2.06 |
3.49 |
-0.6 |
10 |
187 |
14 |
68 |
9.0 |
|
usgs2 |
3.90 |
1.82 |
-0.13 |
-1.69 |
1.34 |
3.17 |
-0.56 |
24 |
193 |
14 |
81 |
9.0 |
|
ipgs |
4.26 |
1.695 |
-0.147 |
-1.548 |
1.403 |
3.637 |
-0.534 |
19.5 |
196 |
12 |
85 |
9.0 |
矩张量的单位是10e22 n.m
harvard 是哈佛大学利用地频面波反演的震源机制解
usgs1是美国usgs利用地震体波反演的震源机制解
usgs2是美国usgs利用w-phase波反演的震源机制解
ipgs 是法国ipgs利用w-phase波反演的震源机制解
我们着重对简正模0s0进行了比较和分析。0s0是径向简正模,其相应的质点振动只有径向运动而没有任何横向运动,在传播过程中不会受到地球自转、地球介质横向不均匀和方位各向异性的影响。因此比较和分析简正模0s0得出的结果比较可靠。图3、4、5的比较结果显示哈佛大学的结果最接近观测值,而美国usgs利用地震体波反演的震源机制解明显大于观测值。0s0的振幅大小与地震矩心矩张量的径向分量mrr以及震源深度有关。usgs1的mrr值最大,震源深度最浅,这是导致其自由震荡模拟值明显大于观测值的主要原因。
根据地震矩心矩张量理论,径向分量mrr=m0*sin(2*dip)*sin(slip)。因此影响0s0的振幅的参数是地震矩标量值m0、断层面倾角dip、断层滑动方向slip以及震源深度depth。表1显示,哈佛大学的震源机制解给出的地震矩标量值m0最大,并由此给出矩震级为mw9.1,但由于其断层面倾角dip最小,导致径向分量mrr较小,使得0s0的振幅明显小于由usgs1震源机制解得到的振幅。
我们进一步的分析表明:对于表1的结果,在m0不变的情况下,dip和slip减小、depth增大会使0s0的振幅变小,其中depth增大50%可导致0s0的振幅约变小5%,slip减小10%可导致0s0的振幅变小不超过1%,而dip减小10%可导致0s0的振幅变小大于10%。因此,断层面倾角dip 对径向分量mrr的影响最大。dip偏大(14o)、depth过小(10km)是导致usgs1的结果严重偏离自由振荡重力观测值的主要原因。
如果哈佛大学的震源机制解给出的断层面倾角是正确的,即dip的值较小(10o),日本仙台大地震的震源深度大约为20km,其震级可能达到mw9.1级。
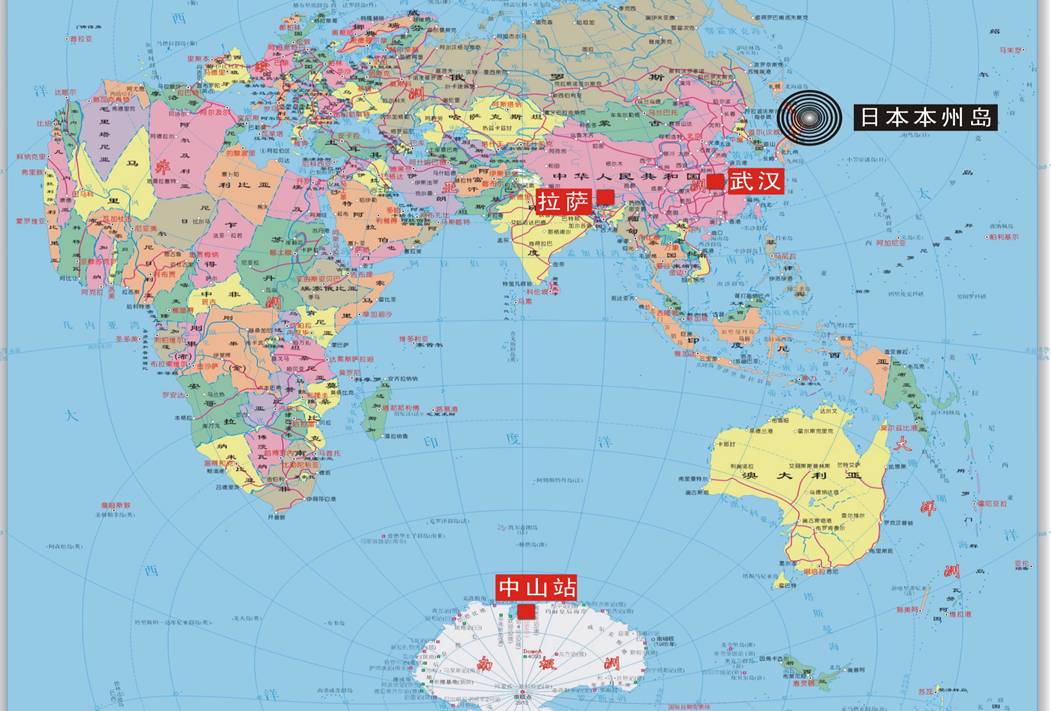
图1中国科院测量与地球物理研究所重力观测站的位置及日本仙台大地震震源位置
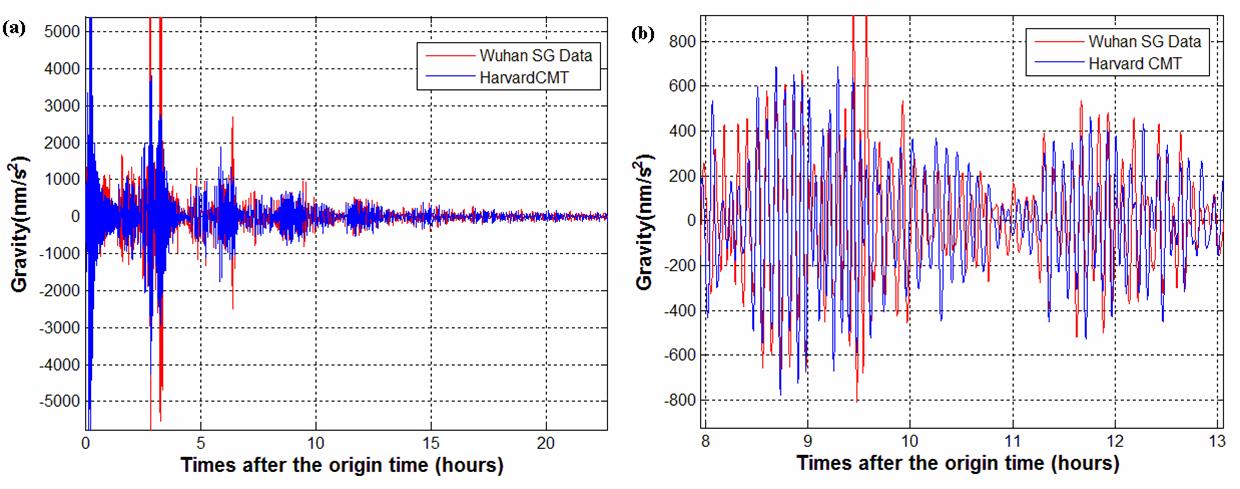
图2(a)为武汉超导重力仪自由振荡观测数据和哈佛震源机制解模拟数据在时间域的比较。(b)为(a)的局部放大图。
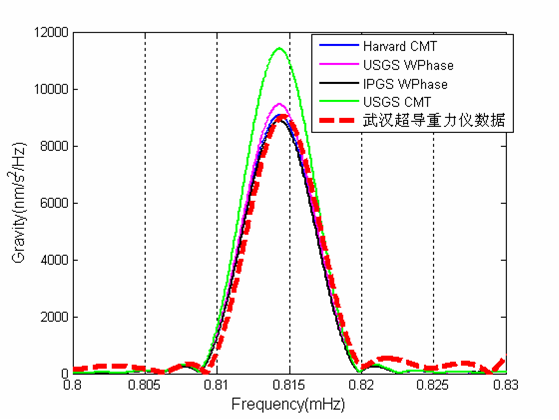
图3 四个震源机制模型模拟计算的武汉九峰台简正模0s0与实际观测数据谱的比较,时间窗为100小时。
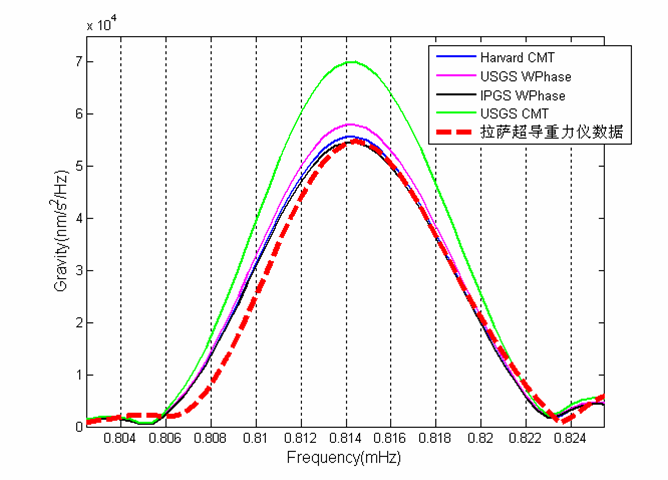
图4 四个震源机制模型模拟计算的拉萨台简正模0s0与实际观测数据谱的比较,时间窗为60小时。
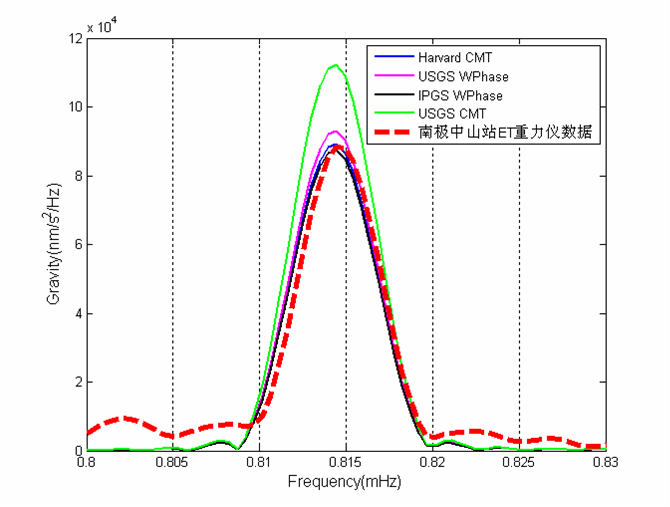
图5 四个震源机制模型模拟计算的南极中山台简正模0s0与实际观测数据谱的比较,时间窗为100小时。

